Puzzel 21 – Set #7

Winnaars vorige keer

#1: Henri – 4 sets
#1: Joran – 1 set
#3: –

Gefeliciteerd Henri!

Kleine regelwijziging

Bij gelijk spel wint degene die de meeste sets in de kaarten A t/m L heeft gevonden. Deze kunnen dus voortaan bij de oplossing vermeld worden.

Oplossing vorige puzzel

De beste oplossing voor de vorige puzzel was Twee blauw gevulde tildes (4 sets). (selecteer de tekst om het antwoord te zien).

U kunt uw antwoorden voor deze week weer insturen door een reactie op dit bericht te geven.

Regels

Een Set-spel heeft 81 kaarten met vier kenmerken: kleur, aantal, vorm en vulling. Bijvoorbeeld: Twee gevulde rode ovalen. Een set is een groep van drie kaarten die per kenmerk allemaal identiek of allemaal verschillend zijn. Een voorbeeld van een set is:

  • Een groen open rechthoek
  • Een groen gestipte ovaal
  • Een groen gevulde tilde

In deze voorbeeldset zijn het aantal en de kleur steeds hetzelfde en de vorm en vulling steeds verschillend. Een uitgebreidere beschrijving van de regels van Set kan hier gevonden worden.

Tabel van mogelijkheden voor de vier kenmerken:

Aantal Kleur Vulling Vorm
Een Rood Open Rechthoek
Twee Groen Gestipt Ovaal
Drie Blauw Gevuld Tilde

Doel van de puzzel is om de kaart met het vraagteken te vervangen met een andere kaart die de meeste extra sets creëert. Deze kaart mag uiteraard niet al op tafel liggen.

In de antwoorden graag de gekozen kaart en de daardoor gecreëerde sets vermelden.

Als voorbeeld: Twee rood gevulde rechthoeken – 3 sets (M-D-G, M-L-E, M-A-K)

De winnaar is degene die de meeste nieuwe sets maakt.

Deadline

De deadline voor het posten van oplossingen is woensdag 15 april 05:00

set_7

3 gedachten over “Puzzel 21 – Set #7”

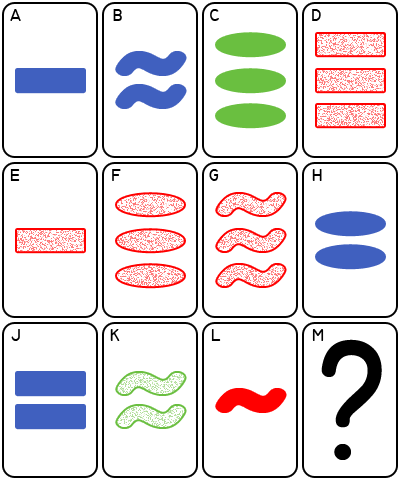
  1. 3 bestaande sets: F-G-D, B-H-J, L-J-C.
    Eén groen leeg ovaal – 4 sets: M-K-C, M-H-F, M-B-F, M-J-G

  2. Joran heeft gereageerd, dus kan ik niet achterblijven met mijn 5 (8) sets.

    Een Groene Open Rechthoek:
    A-E-M
    B-F-M
    C-K-M
    D-J-M
    G-H-M

    Bestaande sets:
    B-H-J
    C-J-L
    D-F-G

  3. m= (1 groen,open,rechthoek)

    nieuwe sets

    1 (a, e, m)
    2 (g, h, m
    3 (f, b, m)
    4(d,j,m)
    5 (m,k,c)

    oude sets

    1 (d,g,f)
    2 (b,h,j)
    3(l,j,c)

    jeroen v eijk

Reacties zijn gesloten.